Profª Socorro F. Osmar - Escola Rio Caeté
segunda-feira, 3 de janeiro de 2011
Turma 104 leva o título
Projeto vencedor na Feira Científico-Pedagógica da Escola Bolívar Bordallo. Parabéns moçada, vocês merecem!É um prazer fazer parte da equipe orientadora.
Equipe vencedora (BBS) comemorando o título. Parabéns!
Meu neto Predro Otávio
Pedro Otávio em traje de marujo homenageia o glorioso São Benedito, Santo amado pelos bragantinos. Pedro você está uma graça!
Gráficos da Função Logarítmica
A representação gráfica da função logarítmica deve ser gravada por todos. Várias questões de vestibular exigem este conhecimento.
A representação gráfica de um logaritmo pode ser de duas formas. Veja os gráficos abaixo mostrando as duas formas para a função :
:
Nestes gráficos devemos observar, principalmente, duas propriedades. Note que os cortes no eixo x, em ambos os gráficos, ocorre no ponto 1. Isso está de acordo com a 1° Consequência da Definição de logaritmos, que diz que logaritmo de 1 em qualquer base é ZERO.
E o eixo y é uma assíntota vertical, ou seja, a curva não toca o eixo y nunca, apenas vai chegando cada vez mais perto, sem tocar.
Veja um exercício do vestibular da UFRGS sobre este tema:
(UFRGS) A representação geométrica que melhor representa o gráfico da função real de variável real x, dada por , é
, é
Devemos saber também que, quanto maior a base de um logaritmo, mais próximo de ambos os eixos estará seu gráfico. Veja a figura ao lado.

(UFRGS) Na figura, a curva S representa o cunjunto solução da equação e a curva T, o conjunto solução da equação
e a curva T, o conjunto solução da equação  . Tem-se
. Tem-se

A representação gráfica de um logaritmo pode ser de duas formas. Veja os gráficos abaixo mostrando as duas formas para a função
| |||||
|
E o eixo y é uma assíntota vertical, ou seja, a curva não toca o eixo y nunca, apenas vai chegando cada vez mais perto, sem tocar.
Veja um exercício do vestibular da UFRGS sobre este tema:
(UFRGS) A representação geométrica que melhor representa o gráfico da função real de variável real x, dada por
| (A) |  | (B) |  | (C) |  |
| (D) |  | (E) |  |
| O enunciado nos diz que o logaritmo pedido possui base igual a Dentre as alternativas, somente as letras A e D são decrescentes, mas somente a alternativa A corta o eixo x no ponto 1. Resposta correta, letra A. |
Devemos saber também que, quanto maior a base de um logaritmo, mais próximo de ambos os eixos estará seu gráfico. Veja a figura ao lado.

(UFRGS) Na figura, a curva S representa o cunjunto solução da equação
 | (A) a < b < 1 (B) 1 < b < a (C) 1 < a < b (D) b < a < 1 (E) b < 1 < a |
| Os dois gráficos representam logaritmos crescentes, ou seja, ambas as bases são maiores do que 1. Ficamos então entre as alternativas B e C. Devemos então saber qual a relação entre a e b. Como a curva S está mais próxima dos eixos x e y do que a curva T, então sua base é maior (a > b). Portanto, resposta correta, letra B. |
gráficos da função exponencial
Para o estudo de vestibular iremos ver bem por cima os gráficos de equações exponenciais.
Existem dois tipos de curvas para o gráfico de uma função exponencial: crescente e decrescente.
E como iremos saber quando uma função exponencial é crescente ou decrescente???
- Isso é fácil! Lembra da nomenclatura de uma potência?
Os nome continuam os mesmos: "a" é a base e "x" é o expoente. São exemplos de funções exponenciais:
 Note que a base de uma função exponencial pode ser qualquer número real, mas para os estudos do vestibular iremos restringir o valor da base somente aos reais positivos. Veja por quê:
Note que a base de uma função exponencial pode ser qualquer número real, mas para os estudos do vestibular iremos restringir o valor da base somente aos reais positivos. Veja por quê:
- Tá, mas como se faz para distinguir funções crescentes ou decrescentes?
Ok, vamos traçar o gráfico das funções f(x)=2x e f(x)=(1/2)x , para isso vamos dar valore para "x" e achar seu correspondente em "y":
Através destes gráficos tiramos a propriedade procuradal
- Uma função exponencial será crescente se sua base for maior que 1 (a>1) ;
- Uma função exponencial será decrescente se sua base for menor que 1, mas sempre positiva (0<a<1).

Existem dois tipos de curvas para o gráfico de uma função exponencial: crescente e decrescente.
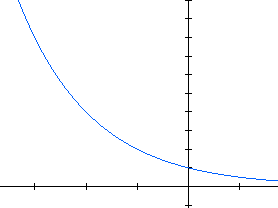 | Este é o gráfico de uma função exponencial decrescente. |
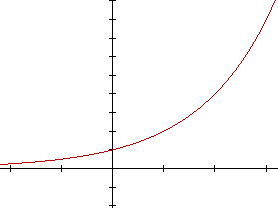 | Este é o gráfico de uma função exponencial crescente. |
- Isso é fácil! Lembra da nomenclatura de uma potência?
Xn
Pois é, nas exponenciais não muda quase nada. Veja só:f(x) = ax
y = ax
A diferença é que antes o expoente era um número. Agora, o expoente será uma função de x. y = ax
Os nome continuam os mesmos: "a" é a base e "x" é o expoente. São exemplos de funções exponenciais:

| Se tivéssemos esta função, por exemplo. Aplicando as propriedades de potenciação teríamos: | |
| Esta seria a função. Uma raiz quadrada de um número negativo não faz parte do conjunto dos REAIS, portanto não é pedido no vestiba. |
Ok, vamos traçar o gráfico das funções f(x)=2x e f(x)=(1/2)x , para isso vamos dar valore para "x" e achar seu correspondente em "y":
y=2x
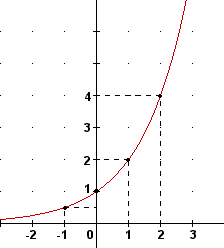 | f(x)=(1/2)x
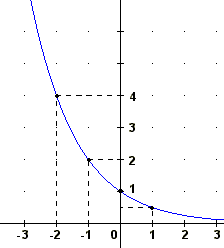 |
- Uma função exponencial será crescente se sua base for maior que 1 (a>1) ;
- Uma função exponencial será decrescente se sua base for menor que 1, mas sempre positiva (0<a<1).
CURIOSIDADE |
| Qualquer gráfico de função exponencial do tipo f(x)=ax passa pelo ponto (0,1), pois qualquer número elevado na potência zero vale 1: a0=1 |
segunda-feira, 27 de dezembro de 2010
atividades para a turma 101(individual)
Resolva as questões abaixo:
1-O numero de bacterias em um meio duplica de hora em hora. Se, inicialmente, existem 8 bacterias no meio, ao fim de 10 horas o número de bacterias será?
2-A cada ano que passa, o valor de um carro diminui de 20% em relação ao ano anterior. Se V for o valor do carro no ano da compra, após 10 anos será?
3-O número de bacterias numa certa cultura duplica a cada hora. Se, num determinado instante, a cultura tem mil bacterias, daí a quanto tempo, aproximadamente, a cultura terá um milhão de bacterias? Considerar log 2 = 0,3.
4-O volume de um liquido diminui de 20% por hora. Após um tempo t, seu volume se reduz a metade. O valor que mais se aproxima de t é? (Use log 2 = 0,30).
1-O numero de bacterias em um meio duplica de hora em hora. Se, inicialmente, existem 8 bacterias no meio, ao fim de 10 horas o número de bacterias será?
2-A cada ano que passa, o valor de um carro diminui de 20% em relação ao ano anterior. Se V for o valor do carro no ano da compra, após 10 anos será?
3-O número de bacterias numa certa cultura duplica a cada hora. Se, num determinado instante, a cultura tem mil bacterias, daí a quanto tempo, aproximadamente, a cultura terá um milhão de bacterias? Considerar log 2 = 0,3.
4-O volume de um liquido diminui de 20% por hora. Após um tempo t, seu volume se reduz a metade. O valor que mais se aproxima de t é? (Use log 2 = 0,30).
terça-feira, 14 de dezembro de 2010
DANÇA: FREVO
III SARAU LITERÁRIO DA ESCOLA RIO CAETÉ (13/12/2010)
Alunos do Projeto Mais Educação
Monitores: Kleidilson e Giovanna Osmar
Ritmo Nordestino: Frevo
A palavra Frevo nasceu da linguagem simples do povo e vem de "ferver", que as pessoas pronunciavam "frever". Frevo é uma música genuinamente pernambucana do fim do seculo XIX - acredita-se que sua origem vem das bandas de música, dobrados e polcas. Segundo alguns é a única composição popular no mundo onde a música nasce com a orquestração. Os passos da dança simbolizam uma mistura de danças de salão da Europa, incluindo passos de ballet e dos cossacos.
Pode-se dizer que o frevo é uma criação de compositores de música nordestina, especialmente para o Carnaval. No decorrer do tempo a música ganhou um gingado inconfundível de passos soltos e acrobáticos.
Podemos dizer que hoje em dia é o ornamento que mais caracteriza o passista e é um dos principais símbolos do carnaval de Pernambuco.
Apesar de parecerem simples e bonito ao olhar, os passos do frevo requerem atenção, equilibrio, mobilidade e disciplina, pois, esta dança envolve movimentos de todo o corpo e inclui: gingados, malabarismos, rodopios, passinhos miúdos e muitos outros passos complicados.
Nós alunos do turno da manha, vinculados ao Projeto Mais Educação queremos mostrar para voces esta dança popular que também representa a cultura nordestina.
Assinar:
Comentários (Atom)








